吴恩达机器学习与深度学习总结。
梯度下降原理
梯度下降算法
代价函数定义
梯度下降算法—求最小代价函数的一种算法,通过不断变幻参数使得找到最小代价函数,代价函数的定义

算法概要

注:a表示学习率下降得多快
算法详解
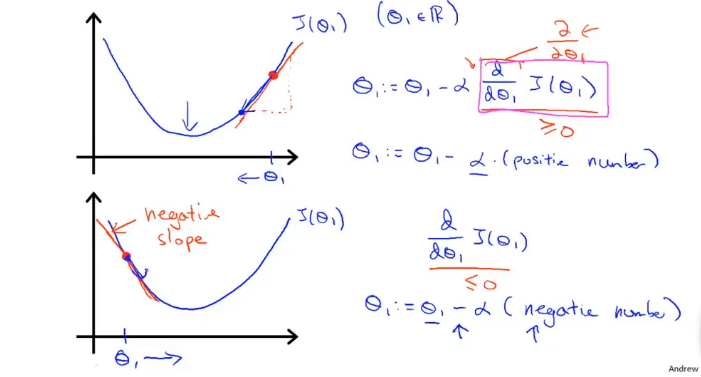
当 在右边时,由于导数为x轴的 与y轴的 的比值,又由于 在右边,故 与 皆为正数所以其导数为正,通过公式,参数会向右趋近。
当 在左边时,由于 为正数与 为负数,故其导数为负数,通过上面公式 ,参数会向左进行趋近,无论 在其极小值的左边或右边皆向极小值逼进,通过一系列的趋近,最终目的是使得参数趋近于最小值。
此算法通过不断迭代直到极小值,当 为极小值点时其导数斜率趋向于某个值 ,此时斜率发生的变化极小
注:我们需要合理调整学习率
当学习率a过大时,会导致过大,就有
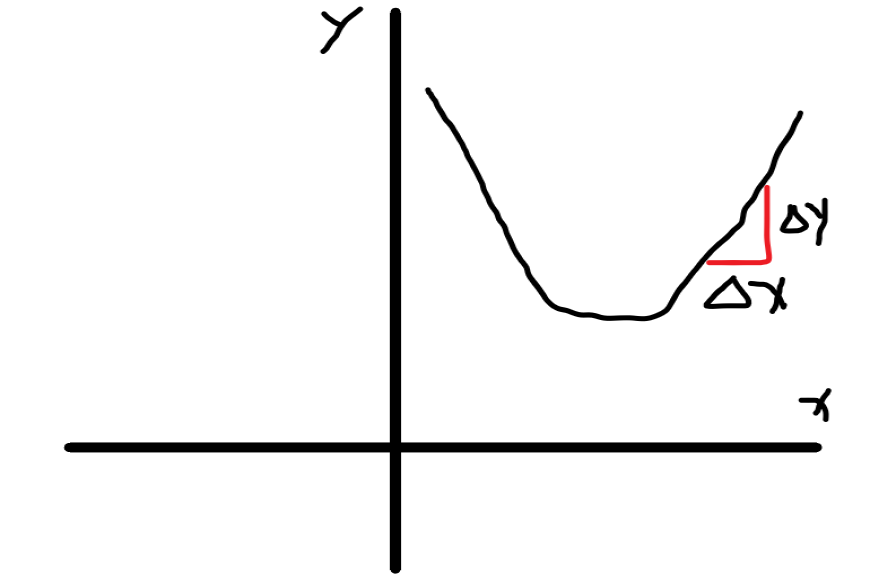
当学习率过大时,会导致
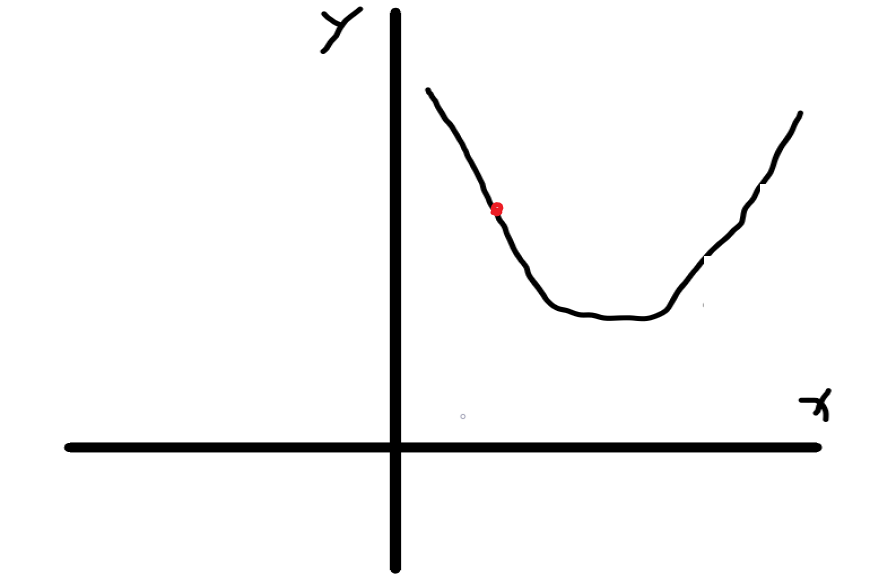
这样会导致从右边直接跨过极小点,直接到左边的位置,这是学习率过大导致的情况。
而若学习率过小会导致需要多次迭代。
神经网络原理
神经网络梯度下降算法

如图所示,我们有参数w,b,代价函数,我们需要通过和来更新梯度下降,使得参数和来更新。
神经网络反向传播详解
神经网络的计算是按照正向传播与反向传播过程来实现的,首先通过正向传播计算出神经网络的输出,紧接着进行一个反向传播,反向传播可以计算出对应的梯度或导数,即正向传播服务于反向传播,反向传播服务于导数的计算。依赖关系导数->反向传播->正向传播。
我们来通过计算图进行分析。
计算图求导数
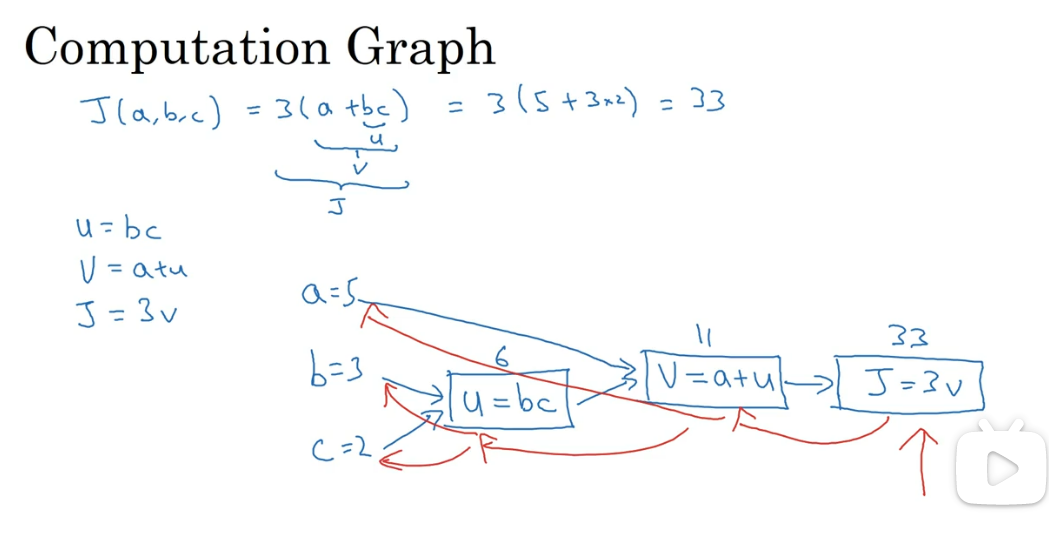
如图我们想要计算函数J(a,b,c)的值,其中
我们计算函数J,可以进行如下步骤的拆分
我们可以得到如下计算图
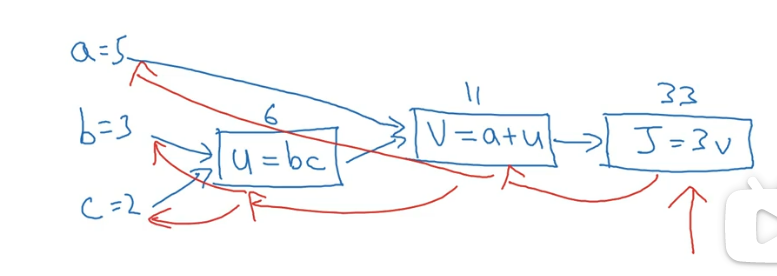
当结果有不同或者一些特殊的输出变量时,比如J也是我们想要优化,在logistic回归中,J也是想要最小化的成本函数,可以看出,一个从左到右的过程,可以计算出函数J的值。接下来我们将会看到为了计算导数数,从右到左的过程。
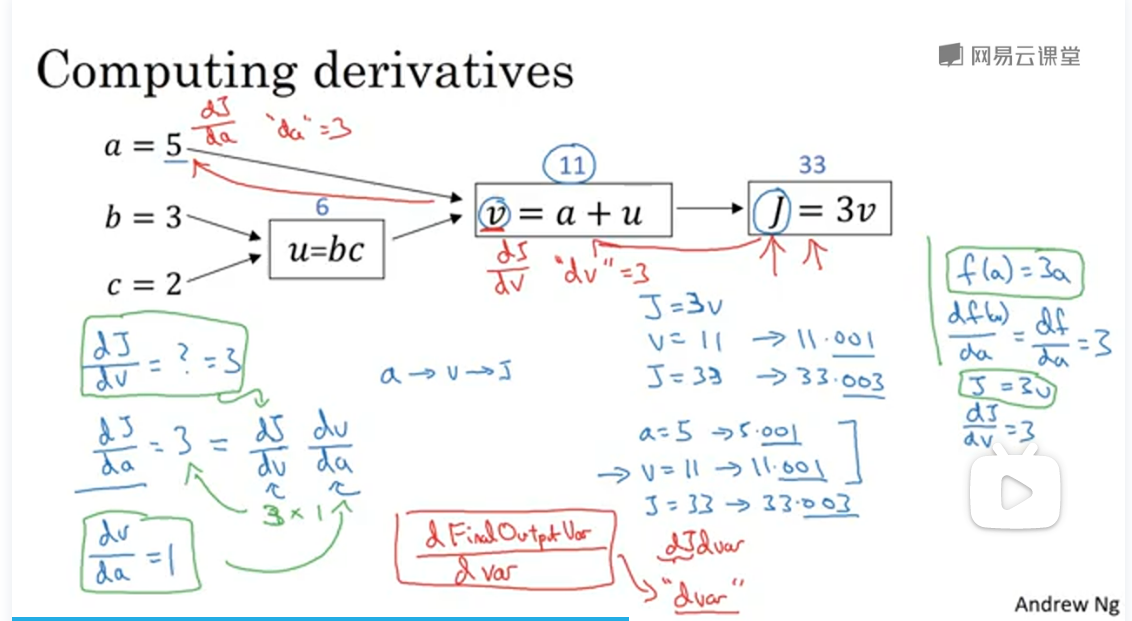
假设我们要计算,我们应该怎么计算呢?
我们若改变V的值,那么J将如何改变呢?
我们有,我们将,变化为V=11.001,而J=33变化为33.003,
即我们可以得到我们在x轴变动1,而 ,我们y轴将变化的动静为x轴的3倍,又当我们令a=5变化成a=5.001, v=11.001, J=33.003,即a的波动影响v, 而影响J,又我们有链式法则 ,即若我们要计算, 需要先计算出 和 。

可以通过上面的方法求出各导数,反向传播原理与上面过程相同。
神经模型
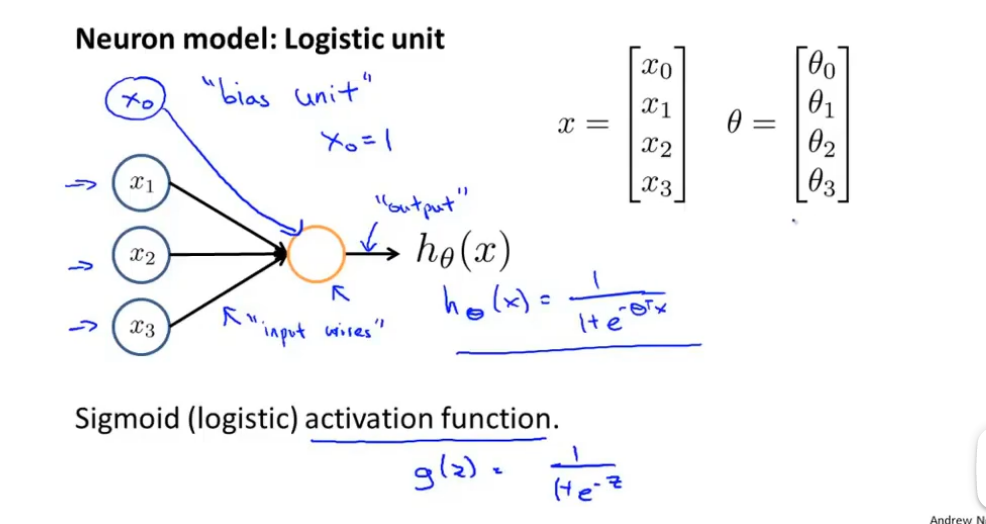
神经模型中的单个逻辑单元如上图所示,通过输入x0,x1,…,xn得到一个逻辑激活函数,这称之为逻辑激活函数 。
逻辑激活函数即
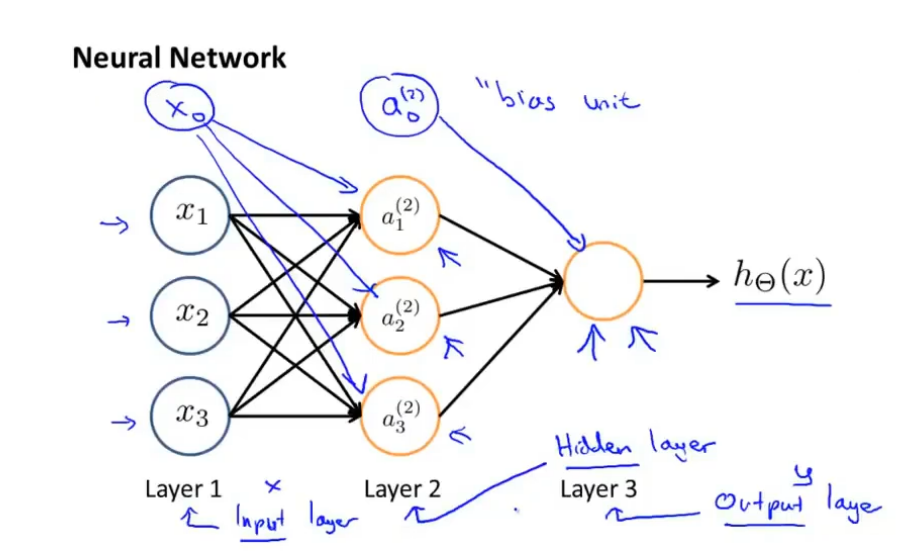
在上图中是由一组神经元组合而成的神经网络,其中最左边的为输入层,中间为隐藏层,最右边的为输出层。

在上图中 示神经网络共有三层,第一层 示输入,中间层 示隐藏层,第三层示输出层。其中 示第j层的第i个激活单元,表示权重控制的矩阵函数从第j 层映射到第 j+1层。如果神经网络在第j层有单元在第j+1层有单元然后有维度
向前传播是指从第一层传播到第三层,以这样的方式进行传播,即从输入层传播到输出层
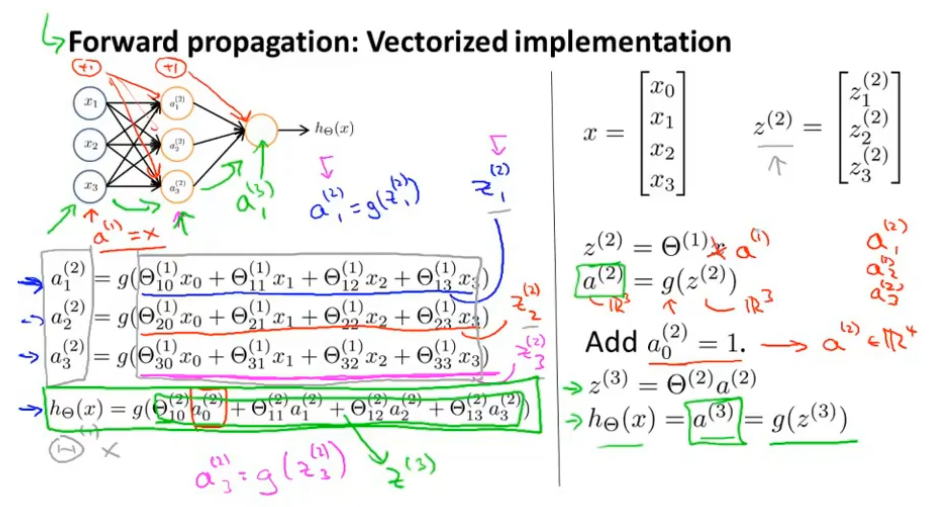
我们对向前传播进行向量化,我们变化为
其中
代价函数
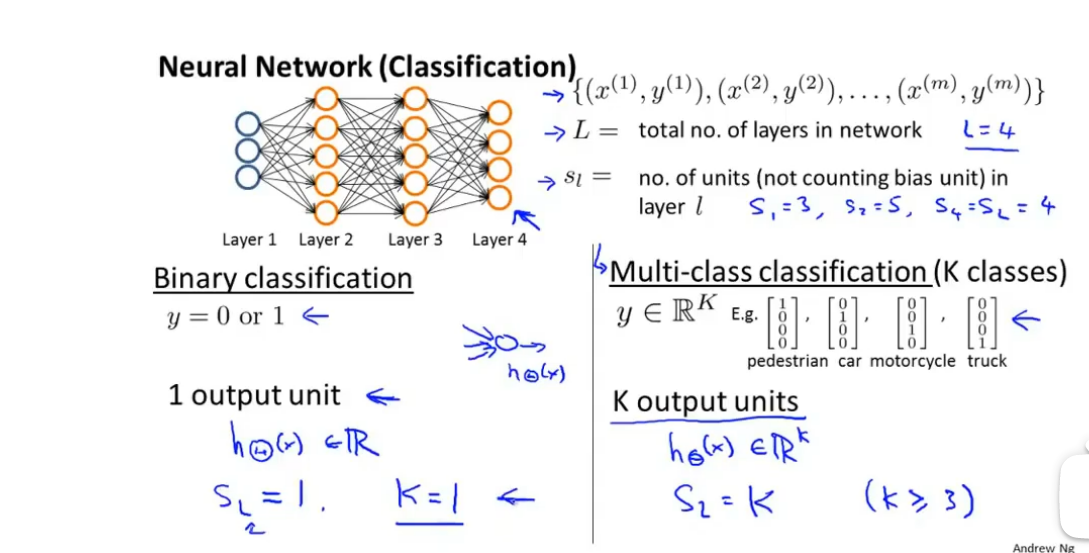
在神经网络中,我们若要实行多元分类,我们需要通过输入样本数据,然后输出数据分类的矩阵,我们需要使得函数来近似于来对不同的数据进行分类。

神经网络的代价函数如下:
其中 表示第i个输出函数,因为在神经网络中有多个输入项,所以有多个代价函数,在这个式子中代价函数数为k,即k个输出函数(项),所以第一项为上式所 示,故有第 一项为
在第二项中, 示有L层,而因为 由上一层与连接下一层而形成的,所以个数也为两层的乘积,而后有从1到L-1,故有第二项为
反向传播过程
反向传播可以计算出在神经网络中各个节点的导数,我们再通过梯度下降算法来进行目标函数的最小化。

在上图中我们的最终目的是寻找最小化
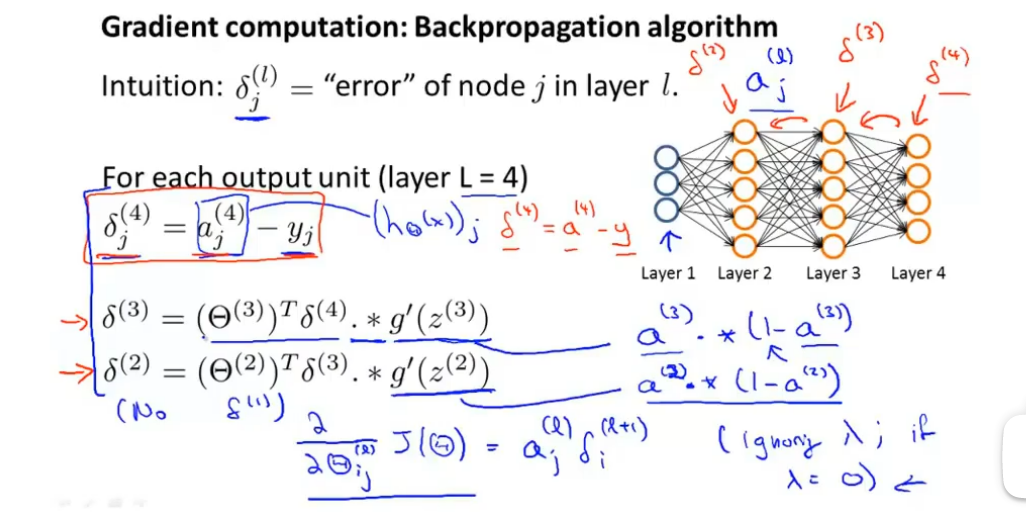
反射传播从直观上来说就是计算每一层的每个节点的误差,在上图中就是计算第三层的各个节点的误差,而后计算第二层的各个节点的误差,最后计算第一层的各个节点的误差,其中
我们有梯度下降的正向传播过程以及涉及的参数如下

梯度下降算法中的反射传播算法过程如下

其中反向传播算法如下:

其中符号,其中l表示神经网络的层数,i表示样本数,j表示神经网络中某层的第几个节点
算法步骤解释如下:
一、设置所有符号均为0.
二、设置从样本1到m的循环,即遍历所有样本.
三、在循环中设置输入参数为.
四、执行正向传播算法,求得各层的.
五、使用结果来计算输出层的差值.
六、计算隐藏层的差值
七、计算每个样本的各层的各个节点的,其中式子
当的m为1,且无正则项时,
八、 我们计算各样本各层节点的,,此处的函数m不等于1且有正则项的分两种情况,当
为什么此时是不是暂时不清楚
反向传播算法的理解与推导
