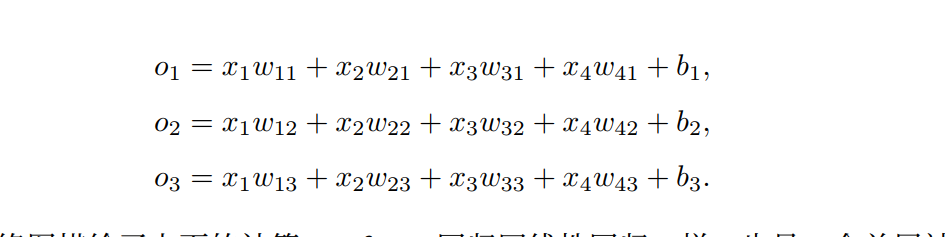本章节为<<动手学深度学习>>的知识点整理。
深度学习基础 线性回归
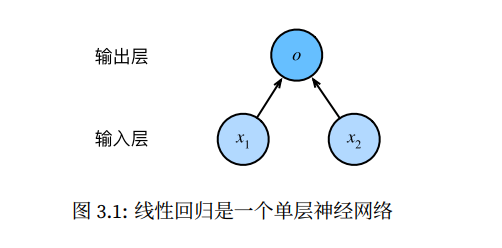
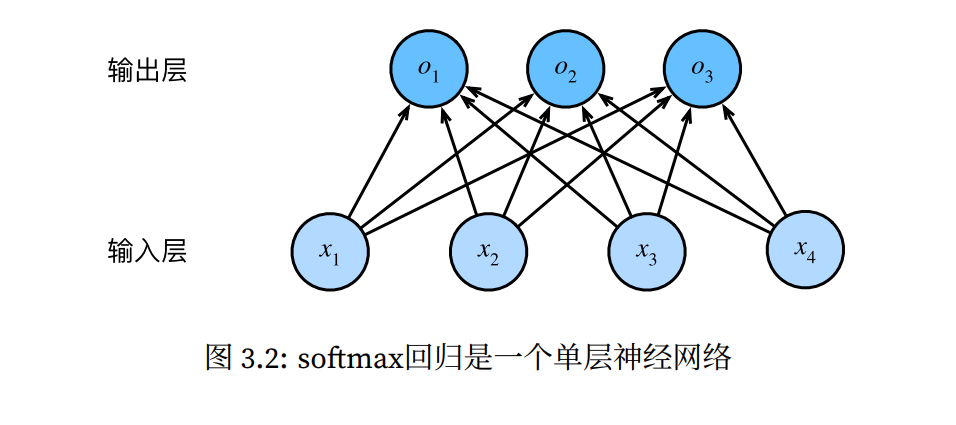
注 :线性回归为一个单层的神经网络
线性回归的基本要素 模型 设房屋面积为x1,房龄为x2,售出价格为y,我们需要建立基于输入x1和x2来计算输出y的表达式,即模型,线性回归假设输出与各个输入之间是线性关系,则我们有公式
其中w1,w2是权重,b是偏差。模型输出
模型训练 我们需要寻找特定的模型的参数值,使得模型在数据上的误差尽可能的小。
训练数据 我们收集一系列的数据,在这个数据上面寻找模型参数来使得模型的预测价格与真实价格的误差最小。这个数据集被称之为训练集。
假设我们采集的样本数为n,索引为i的样本的特征为
损失函数 在模型训练中,我们需要衡量价格预测与真实值之间的误差,通常会选取一个非负作为误差,且数值越小表示误差越小,一个常用的式子为
其中常数1/2使对平方项求导后的常数系数为1,这样在形式上稍微简单,其中这个式子的误差越小表示预测价格与真实价格越相近。
通常我们用训练数据集中所有样本误差的平均来衡量模型预测的质量,即
在模型的训练中,我们希望找出一组模型参数,记为$ w^_1 _2
优化算法 我们通过小批量随机梯度下降法,来进行求出最优的$ w^_1 _2
批量梯度下降算法:在每次迭代中使用所有样本
随机梯度下降算法:在每次迭代中使用一个样本
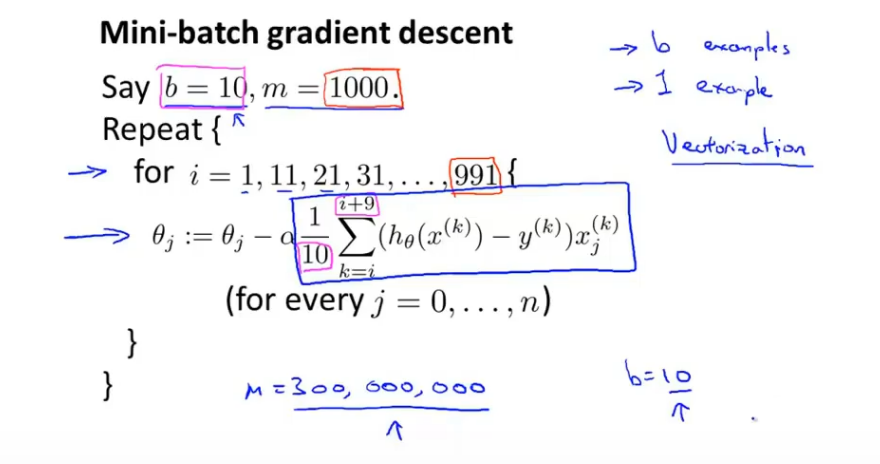
Mini-Batch梯度下降算法:在每次迭代中使用b个样本
图中是B为10的一个例子,Mini-batch在数据存取和求导的过程中使用向量化,进行并行计算,这样可以加快计算速度,而Mini-batch的一个缺点是需要确定参数B的大小。
对于上例中我们有算法
1 2 3 Repeat { for i=1 ,i=b+1 ,i=2b+1 ,...n{
线性回归的表示方法 我们对训练数据集里的3个房屋样本(索引分别为1、2和3)逐一预测价格,将得到
将上面3个等式转化成矢量计算,则有
当数据样本数为n,特征数为d时,线性回归的矢量计算表达式为
其中模型输出$y^\in R^{n 1}, 批 量 数 据 样 本 特 征 d}, 权 重 1}, 偏 差 , 批 量 数 据 样 本 标 签 , 设 模 型
小批量随机梯度下降可以改写为
线性回归从零开始实现 设我们训练数据集样本数为1000,输入个数(特征数)为2。给定随机生成的批量样本特征
其中噪声项
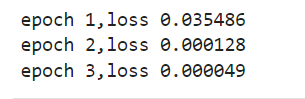
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 num_inputs =2 #特征项数num_examples =1000 #样本数true_w=[2,-3.4] true_b =4.2features =nd.random.normal(scale=1,shape(num_examples,num_inputs)) #生成1000*2 个为1的标准差labels =true_w[0]*fea tures[:,0]+true_w[1]*fea tures[;,1]+true_blables+=nd.random.normal(scale =0.01,shape=labels.shape) # def data_iter(batch_size,features,labels): num_examples =len(features) indices =list(range(num_examples)) #生成样本数量个随机数 random.shuffle(indices) #样本的读取顺序是随机的 for i in range(0,num_examples,batch_size): j =nd.array(indices[i:min(i+batch_size,num_examples)]) yield features.take(j),labels.take(j) #take函数根据索引返回对应元素 w =nd.random.normal(scale=0.01,shape=(num_inputs,1))b =nd.zeros(shape=(1,))w.attach_grad() b.attach_grad() def linreg(X,w,b): return nd.dot(X,w)+b def squared_loss(y_hat,y): return (y_hat-y.reshape(y.hat.shape))**2 /2 def sgd(params,lr,batch_size): for param in params: param[:]=param-lr*param.grad/batch_size lr =0.03 #学习率num_epochs =3 #迭代周期net =linreg loss =squared_lossfor epoch in range(num_epochs):#训练模型一共需要num_epochs个迭代周期 #在每一个迭代周期中,会使用训练数据集中所有样本一次(假设样本数能够被批量大小整除)。 #x和y分别是小批量样本的特征和标签 for X,y in data_iter(batch_size,features,labels): with autograd.record(): l =loss(net(X,w,b),y) #l是有关小批量x和y的损失 l.backward() #小批量的损失对模型参数求梯度 sgd([w,b],lr,batch_size) #使用小批量随机梯度下降迭代模型参数 train_l =loss(net(features,w,b),labels) print ('epoch %d,loss %f' % (epoch+1,train_l.mean().asnumpy()))
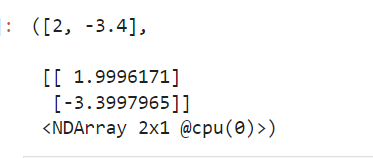
通过上面的计算,我们得到结果(true_w为刚开始定义的值,w为我们通过计算得出的值)
通过以上结果我们可以知道,以上算法是通过优化目标模型来反向求得参数,使得求得的参数最接近原参数。
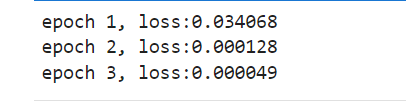
线性回归的简洁实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 from mxnet import autograd,ndnum_inputs =2num_examples =1000true_w=[2,3.4] true_b =4.2features =nd.random.normal(scale=1,shape=(num_examples,num_inputs))labels =true_w[0]*fea tures[:,0]+true_w[1]*fea tures[:,1]+true_blabels+=nd.random.normal(scale =0.01,shape=labels.shape) from mxnet.gluon import data as gdatabatch_size =10dataset =gdata.ArrayDataset(features,labels)data_iter =gdata.DataLoader(dataset,batch_size,shuffle=True)from mxnet.gluon import nnnet =nn.Sequential()net.add (nn.Dense(1)) from mxnet import init net.initialize(init.Normal(sigma =0.01)) from mxnet.gluon import loss as glossloss =gloss.L2Loss() #平方损失又称L2范数损失from mxnet import gluontrainer =gluon.Trainer(net.collect_params(),'sgd',{'learning_rate' :0.03})num_epochs =3;for epoch in range(1,num_epochs+1): for X,y in data_iter: with autograd.record(): l =loss(net(X),y) l.backward() trainer.step (batch_size) l =loss(net(features),labels) print ('epoch %d, loss:%f' % (epoch,l.mean().asnumpy()))
下面我们分别比较学到的模型参数与真实的模型参数,从而从net获得需要的层,并访问其权重和偏差。
1 2 dense =net[0 ]true_w ,dense.weight.data ()
1 true_b ,dense.bias.data ()
图像分类数据集(Fashion-MNIST) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 %matplotlib inline import d2lzh as d2lfrom mxnet.gluon import data as gdataimport sysimport timemnist_train=gdata.vision.FashionMNIST(train=True ) mnist_test=gdata.vision.FashionMNIST(train=False ) feature,label=mnist_train[0 ] feature.shape,feature.dtype label,type (label),label.dtype def get_fashion_mnist_labels (labels ): text_labels=['t-shirt' ,'trouser' ,'pullover' ,'dress' ,'coat' , 'sandal' ,'shirt' ,'sneaker' ,'bag' ,'ankle boot' ] return [text_labels[int (i)] for i in labels] def show_fashion_mnist (images,labels ): d2l.use_svg_display() _,figs=d2l.plt.subplots(1 ,len (images),figsize=(12 ,12 )) for f,img,lbl in zip (figs,images,labels): f.imshow(img.reshape((28 ,28 )).asnumpy()) f.set_title(lbl) f.axes.get_xaxis().set_visible(True ) f.axes.get_yaxis().set_visible(True ) X,y=mnist_train[0 :9 ] show_fashion_mnist(X,get_fashion_mnist_labels(y))
softmax回归从零开始实现 1 2 3 4 5 6 7 %matplotlib inline import d2lzh as d2lfrom mxnet import autograd,nd#设置批处理大小,且导入数据到训练集与测试集中 batch_size=256 train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)
1 2 3 4 5 6 7 8 9 num_inputs =784num_outputs =10w =nd.random.normal(scale=0.01,shape=(num_inputs,num_outputs))b =nd.zeros(num_outputs)w.attach_grad() b.attach_grad()
1 2 3 4 5 6 7 8 9 def softmax (X ): X_exp=X.exp() partition=X_exp.sum (axis=1 ,keepdims=True ) return X_exp/partition
1 2 3 def net (X ): return softmax(nd.dot(X.reshape((-1 ,num_inputs)),w)+b)
1 2 3 4 5 def cross_entropy (y_hat,y ) return -nd.pick(y_hat,y).log()
上面的损失函数等价于,其余部分后面实现
1 2 3 4 5 def accuracy (y_hat,y ): return (y_hat.argmax(axis=1 )==y.astype('float32' )).mean().asscalar()
1 2 3 4 5 6 7 def evaluate_accuracy(data_iter,net): acc_sum,n=0.0 ,0 for X,y in data_iter: y=y.astype ('float32' ) acc_sum+=(net (X).argmax (axis=1 )==y).sum ().asscalar () n+=y.size return acc_sum/n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 num_epochs,lr =5,0.1 def train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,params =None,lr=None,trainer=None): for epoch in range(num_epochs): train_l_sum,train_acc_sum,n =0.0,0.0,0 for X,y in train_iter: #train_iter 返回图像和标签 with autograd.record(): y_hat =net(X) #自己的y值 l =loss(y_hat,y).sum() l.backward() #求导 if trainer is None: d2l.sgd(params,lr,batch_size) #之前定义的小型梯度下降 else : trainer.step (batch_size) y =y.astype('float32') train_l_sum+=l.asscalar() train_acc_sum+=(y_hat.argmax(axis =1)==y).sum().asscalar() n+=y.size test_acc =evaluate_accuracy(test_iter,net) print ('epoch %d,loss %.4f,train acc %.3f,test acc %.3f' %(epoch+1,train_l_sum/n,train_acc_sum/n,test_acc))
1 train_ch3(net ,train_iter ,test_iter ,cross_entropy ,num_epochs ,batch_size ,[w ,b ],lr )
1 2 3 4 5 6 7 8 #给定⼀系列图像(第三⾏图像输出),我们⽐较⼀下它们的真实标签(第⼀⾏⽂本输出)和模型预测结果(第⼆⾏⽂ #本输出) for X,y in test_iter: break true_labels=d2l.get_fashion_mnist_labels (y.asnumpy ()) pred_labels=d2l.get_fashion_mnist_labels (net (X).argmax (axis=1 ).asnumpy ()) titels=[true+'\n' +pred for true,pred in zip(true_labels,pred_labels)] d2l.show_fashion_mnist (X[0:9] ,titels[0:9] )
softmax回归简洁实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 %matplotlib inline import d2lzh as d2l from mxnet import autograd,ndfrom mxnet import gluon,initfrom mxnet.gluon import loss as gloss,nnbatch_size =256train_iter,test_iter =d2l.load_data_fashion_mnist(batch_size) net =nn.Sequential()net.add (nn.Dense(10)) net.initialize(init.Normal(sigma =0.01)) loss =gloss.SoftmaxCrossEntropyLoss()trainer =gluon.Trainer(net.collect_params(),'sgd',{'learning_rate' :0.1})num_epochs =5d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,None,None,trainer)
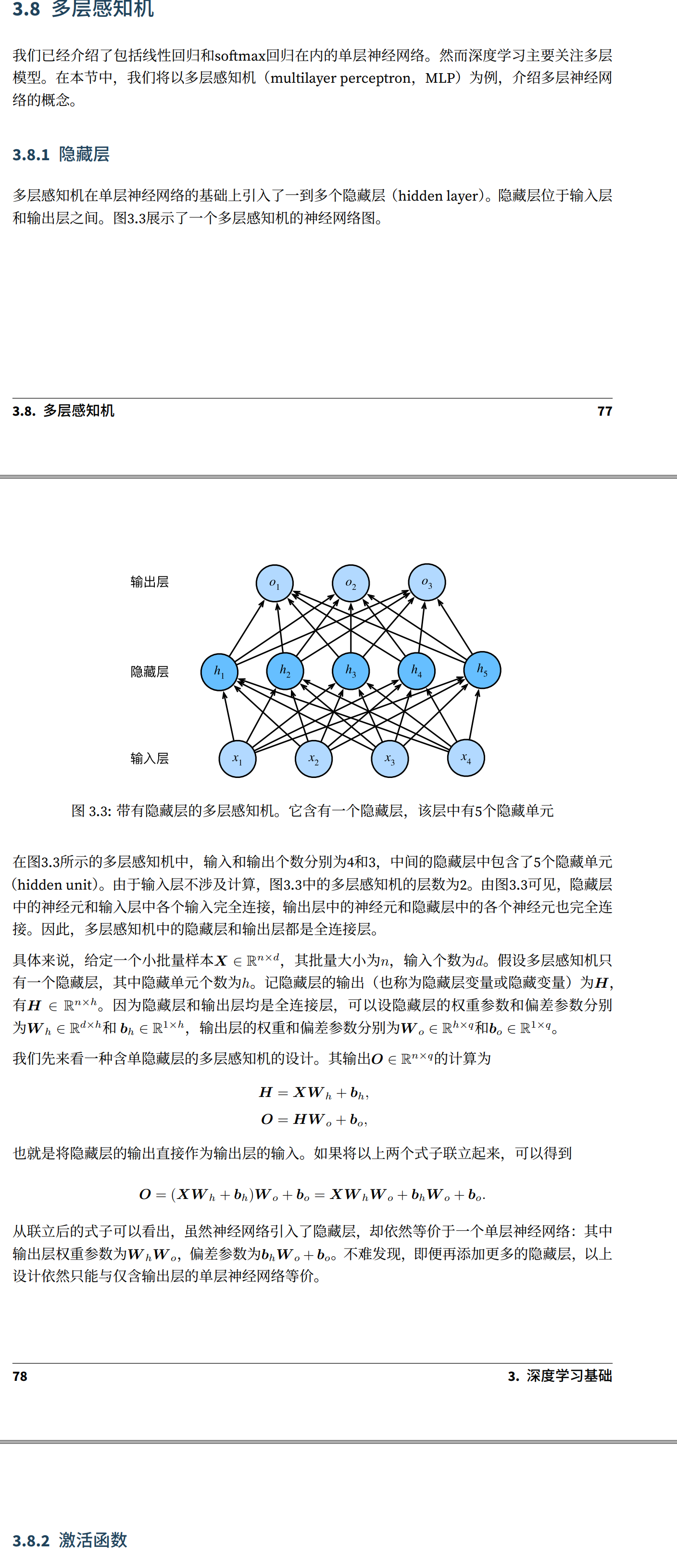
多层感知机
激活函数
多层感知机的从零开始实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 %matplotlib inline import d2lzh as d2l from mxnet import nd from mxnet.gluon import loss as glossbatch_size =256train_iter,test_iter =d2l.load_data_fashion_mnist(batch_size) num_inputs,num_outputs,num_hiddens =784,10,256 W1 =nd.random.normal(scale=0.01,shape=(num_inputs,num_hiddens))b1 =nd.zeros(num_hiddens)W2 =nd.random.normal(scale=0.01,shape=(num_hiddens,num_outputs))b2 =nd.zeros(num_outputs)params=[W1,b1,W2,b2]
多层感知机的简洁实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import d2lzh as d2l from mxnet import gluon,initfrom mxnet.gluon import loss as gloss,nnnet =nn.Sequential()net.add (nn.Dense(256,activation ='relu' ),nn.Dense(10)) net.initialize(init.Normal(sigma =0.01)) batch_size =256train_iter,test_iter =d2l.load_data_fashion_mnist(batch_size) loss =gloss.SoftmaxCrossEntropyLoss()trainer =gluon.Trainer(net.collect_params(),'sgd',{'learning_rate' :0.5})num_epochs =5d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,None,None,trainer)
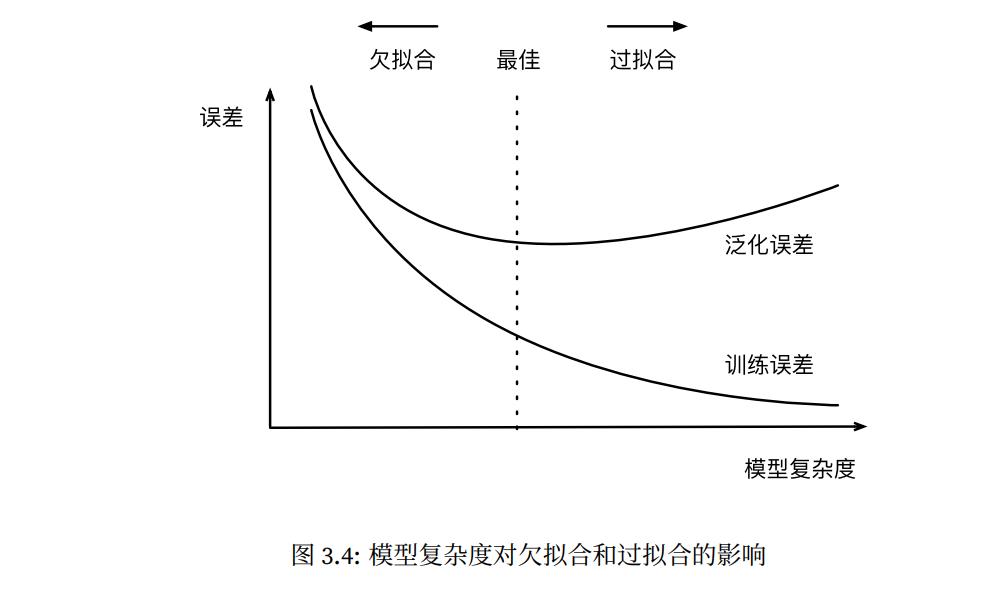
欠拟合与过拟合 给定一个由标量数据特征x和对应的标题标签y组成的训练数据集,多项式函数拟合的目标是找一个K项多项式的函数
来近似,在上式中,的模型的权重参数,b是偏差参数。
因为⾼阶多项式函数模型参数更多,模型函数的选择空间更⼤,所以⾼阶多项式函数⽐低阶多项式函数的复杂度更⾼。因此,⾼阶多项式函数⽐低阶多项式函数更容易在相同的训练数据集上得到更低的训练误差。给定训练数据集,模型复杂度和误差之间的关系通常如图3.4所⽰。给定训练数据集,如果模型的复杂度过低,很容易出现⽋拟合;如果模型复杂度过⾼,很容易出现过拟合。应对⽋拟合和过拟合的⼀个办法是针对数据集选择合适复杂度的模型。
影响⽋拟合和过拟合的另⼀个重要因素是训练数据集的⼤小。⼀般来说,如果训练数据集中样本数过少,特别是⽐模型参数数量(按元素计)更少时,过拟合更容易发⽣。此外,泛化误差不会随训练数据集⾥样本数量增加而增⼤。因此,在计算资源允许的范围之内,我们通常希望训练数据集⼤⼀些,特别是在模型复杂度较⾼时,如层数较多的深度学习模型。
1 2 3 4 5 6 7 8 9 10 11 12 13 %matplotlib inline import d2lzh as d2lfrom mxnet import autograd,gluon,ndfrom mxnet.gluon import data as gdata,loss as gloss,nnn_train,n_test,true_w,true_b=100 ,100 ,[1.2 ,-3.4 ,5.6 ],5 features=nd.random.normal(shape=(n_train+n_test,1 )) #拼接,ploy_featuers=x,x^2 ,x^3 ploy_features=nd.concat(features,nd.power(features,2 ),nd.power(features,3 )) #y=1.2x-3.4x^2+5.6x^3+5 labels=(true_w[0 ]*ploy_features[:,0 ]+true_w[1 ]*ploy_features[:,1 ]+true_w[2 ]*ploy_features[:,2 ]+true_b) #y+=噪声项 labels+=nd.random.normal(scale=0.1 ,shape=labels.shape)
1 2 3 4 5 6 7 8 9 def semilogy (x_vals,y_vals,x_label,y_label,x2_vals=None ,y2_vals=None ,legend=None ,figsize=(3.5 ,2.5 ): d2l.set_figsize(figsize) d2l.plt.xlabel(x_label) d2l.plt.ylabel(y_label) d2l.plt.semilogy(x_vals,y_vals) if x2_vals and y2_vals: d2l.plt.semilogy(x2_vals,y2_vals,linestyle=':' ) d2l.plt.legend(legend)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 num_epochs,loss =100,gloss.L2Loss() def fit_and_plot(train_features,test_features,train_labels,test_labels): net =nn.Sequential() net.add (nn.Dense(1)) #单层神经网络,一个输出单元 net.initialize() #初始化参数 batch_size =min(10,train_labels.shape[0]) train_iter =gdata.DataLoader(gdata.ArrayDataset(train_features,train_labels),batch_size,shuffle=True) trainer =gluon.Trainer(net.collect_params(),'sgd',{'learning_rate' :0.01}) train_ls,test_ls=[], [] for _ in range(num_epochs): for X,y in train_iter: with autograd.record(): l =loss(net(X),y) l.backward() trainer.step (batch_size) train_ls.append(loss(net(train_features),train_labels).mean().asscalar()) test_ls.append(loss(net(test_features),test_labels).mean().asscalar()) print ('final epoch:train loss' ,train_ls[-1],'test loss' ,test_ls[-1]) semilogy(range(1,num_epochs+1),train_ls,'epochs' ,'loss' ,range(1,num_epochs+1),test_ls,['train' ,'test' ]) print ('weight:' ,net[0].weight.data().asnumpy(),'\nbias:' ,net[0].bias.data().asnumpy())
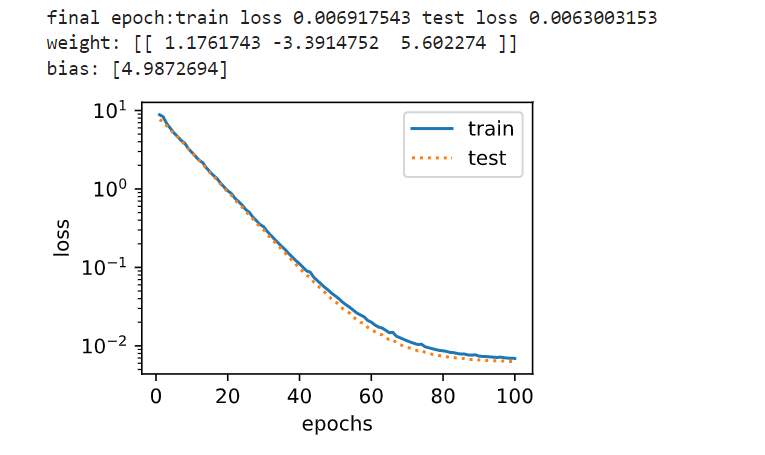
1 2 3 4 5 #三阶多项式函数拟合(正常) #我们先使⽤与数据⽣成函数同阶的三阶多项式函数拟合。实验表明,这个模型的训练误差和在测 #试数据集的误差都较低。训练出的模型参数也接近真实值: w1 = 1 :2 ; w2 = −3 :4 ; w3 = 5 :6 ; b = 5 。 #ploy_features[:n_train ,:] 取前100 个元素,ploy_features[n_train :,:] 取后100 个元素 fit_and_plot(ploy_features [:n_train ,:],ploy_features [n_train :,:],labels [:n_train ],labels [n_train :])
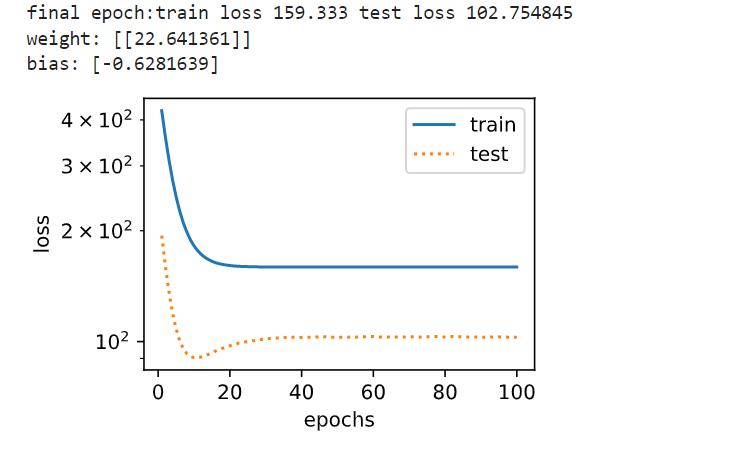
1 2 3 #线性函数拟合(欠拟合) #这个地方,生成的函数是线性的,所以有欠拟合状态 fit_and_plot(features [:n_train ,:],features [n_train :,:],labels [:n_train ],labels [n_train :])
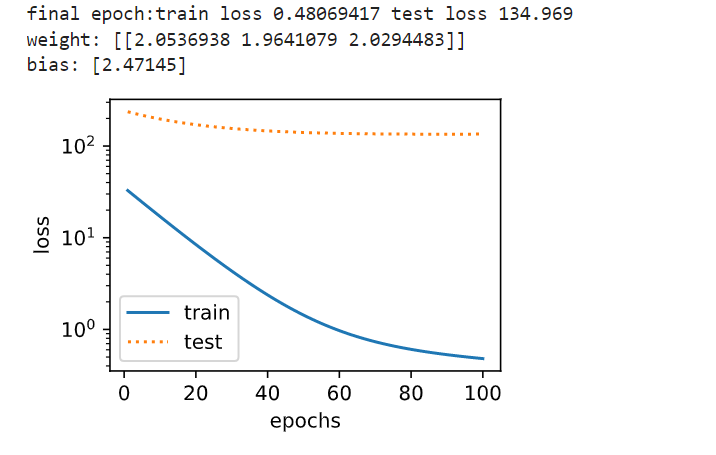
1 2 #训练样本不足(过拟合) fit_and_plot(ploy_features [0:2,:],ploy_features [n_train :,:],labels [0:2],labels [n_train :])
权重衰减-原理暂不解释
在上图中我们的更新公式为
P(w_1,w_2,…,w_t)
P(w_1,w_2,…,w_t)=\prod_{t=1}^Tp(w_t|w_1,…,w_{t-1})
(Y^{})^{}=H_t W_{hq}+b
$$
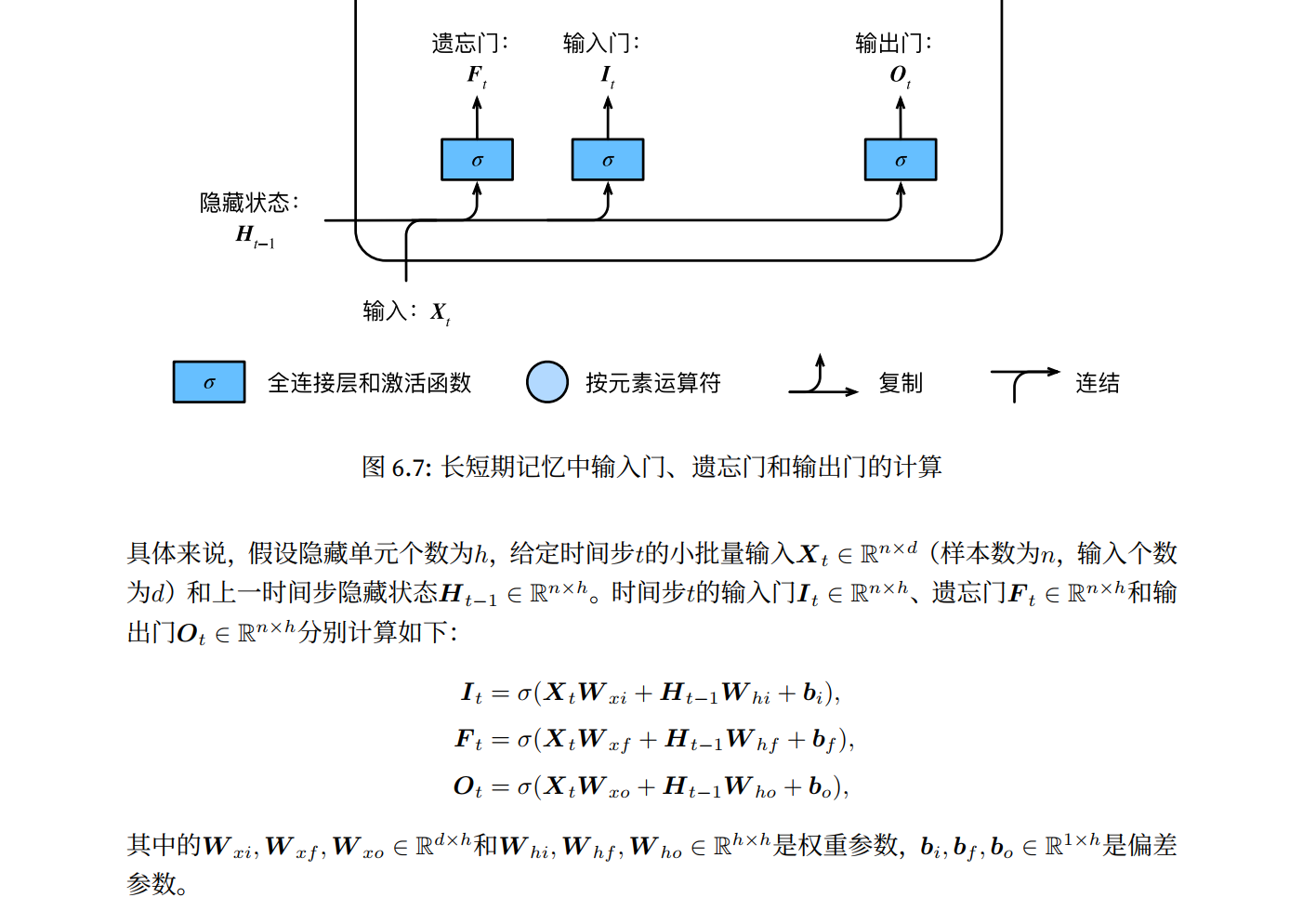
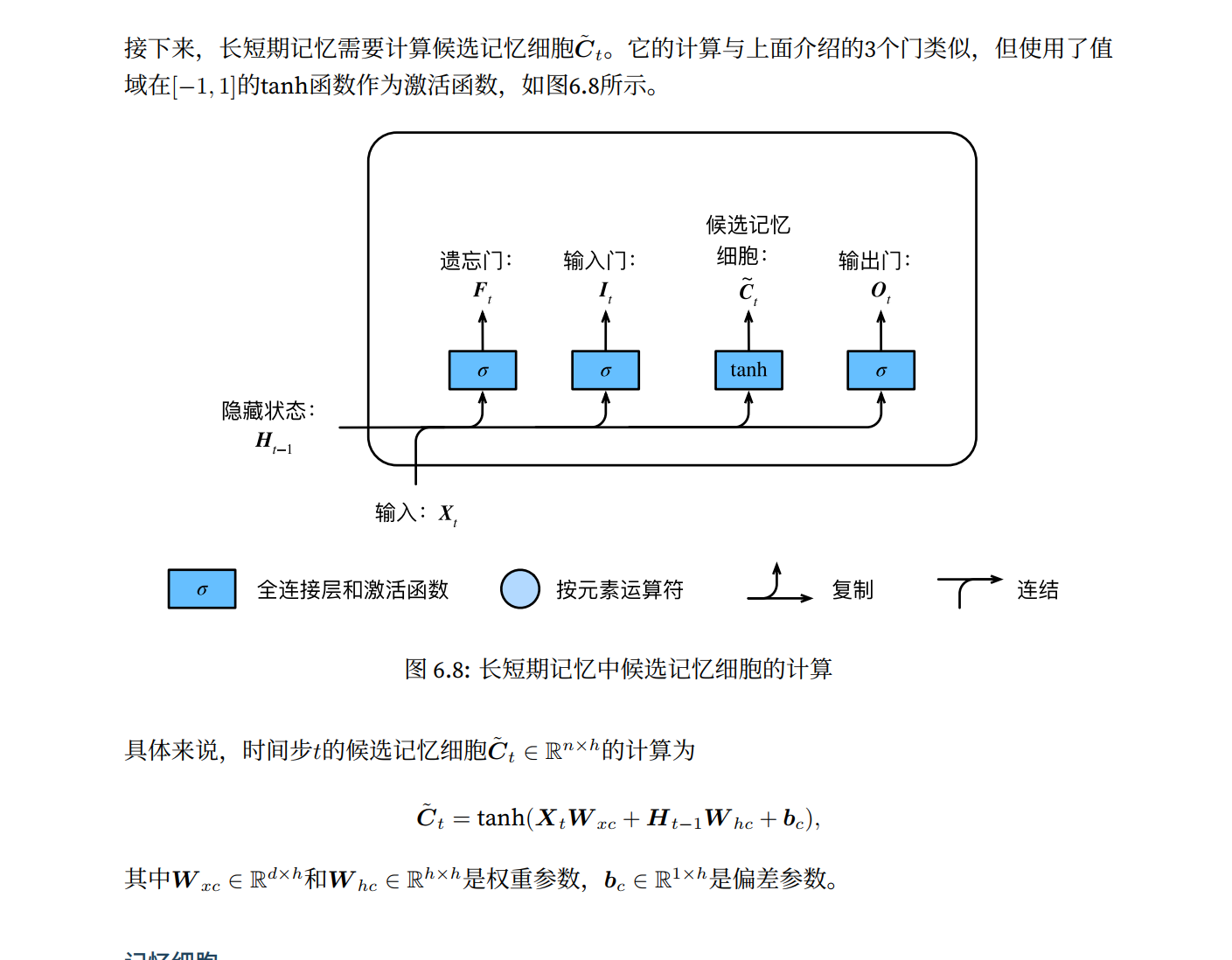
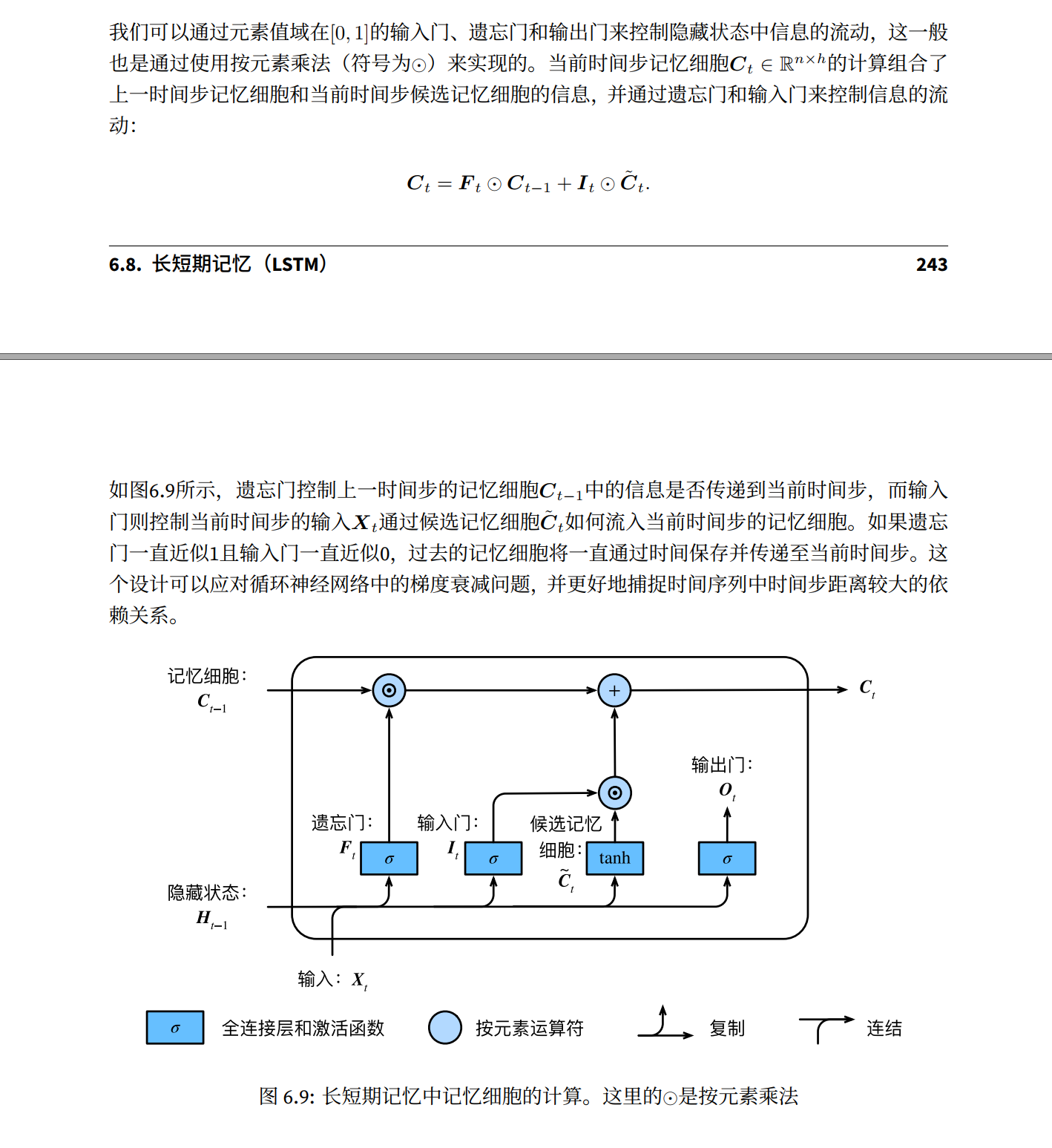
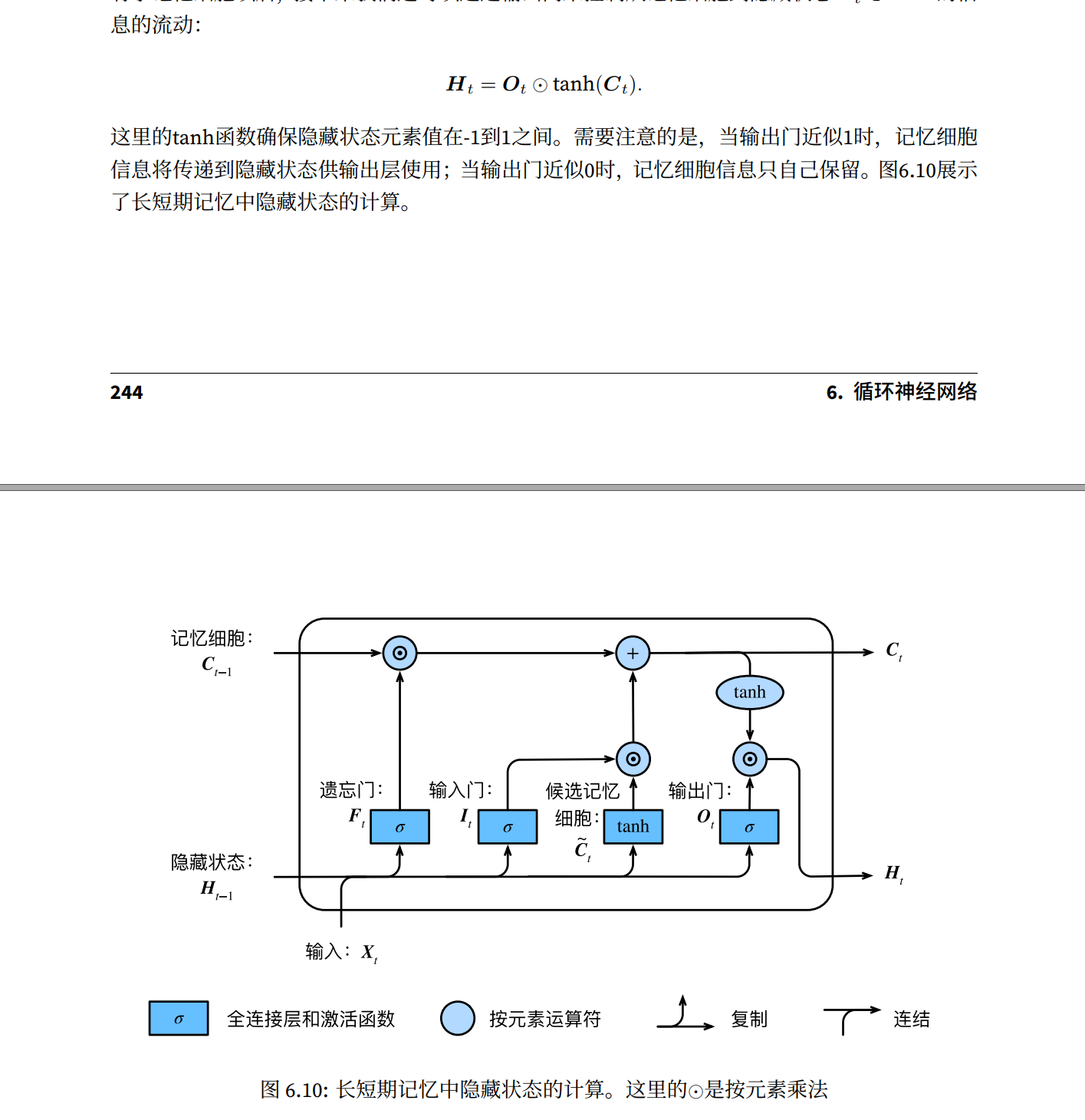
长短期记忆